Fluidodinâmica computacional e suas aplicações
- Introdução
- Modelagem matemática
- Acoplamento pressão-velocidade
- Métodos de discretização
- Modelos de turbulência
- Metodologia les
- Pacotes computacionais
- Resultados
- Discussão e conclusões
- Agradecimentos
- Referências bibliográficas
RESUMO
A Dinâmica dos Fluidos é um ramo da ciência que envolve estudos ligados a problemas de fluidodinâmica, termodinâmica, hidráulica, e outros. Em muitas indústrias, os produtos estão relacionados diretamente com a Dinâmica dos Fluidos e se investe grandes quantidades de recursos para desenvolver novas tecnologias na área de Dinâmica dos Fluidos Computacional e Experimental. Contudo o investimento para a obtenção de resultados experimentais é muito dispendioso, e, devido a isto, vem se investindo muito em modelagem matemática e simulação numérica para obtenção destes resultados, sendo chamado este método de Dinâmica dos Fluidos Computacional, ou a sigla em Inglês CFD (Computacional Fluid Dynamics). Esta metodologia é barata e que gera resultados muito satisfatórios. Assim, o presente trabalho visa dar uma visão geral sobre CFD, e os modelos matemáticos utilizados por ela.
PALAVRAS CHAVE: Simulação Numérica, Dinâmica dos Fluidos Computacional, Modelos Matemáticos.
ABSTRACT
The Fluid Dynamics is a branch of the science where the problems of fluid dynamics, thermodynamics, hydraulical, and others are treated. There are many industries with products that are related directly with the Fluid Dynamics. There is great amounts of resource engaged to develop new technologies in this area. However the investment for the attainment of experimental results is very expensive. So, a high amount of effort has been dedicated to mathematical modeling and numerical simulation for attainment of these results. This area is called Computacional Fluid Dynamics (CFD). Thus, the present work aims at to give a general vision on CFD, and the mathematical models used in this domain.
KEY WORDS: Simulation, Computacional Fluid Dynamics, Mathematical Models
A Fluidodinâmica computacional é uma área de grande interesse para a solução de muitos problemas práticos. Como exemplo, podem ser citados problemas de aerodinâmica, termodinâmica, hidráulica, dentre outros.
As análises nesta área de pesquisa podem ser desenvolvidas com base em experimentos bem como em métodos teóricos. Dentro dos métodos teóricos destacam-se os métodos computacionais, utilizados para simulação numérica aplicada à Dinâmica dos Fluidos.
Para os escoamentos de fluidos, o modelo matemático é estabelecido com base nas equações de conservação da quantidade de movimento, da massa e da energia.
Estas equações, quando submetidas a condições de contorno e iniciais apropriadas, representam, matematicamente, um problema particular (Shames, Irving Herman, 1973). A solução analítica destas equações somente é possível para escoamentos muito simples. Para se analisar problemas reais, lança-se mão do uso dos chamados métodos numéricos.
Nos casos de escoamentos laminares, os modelos são relativamente simples, pois as equações de Navier-Stokes, conservação da massa e conservação de energia são resolvidas. Contudo, como a maioria dos escoamentos que acontecem na natureza e no meio industrial são turbulentos, estes tem um alto grau de complexidade, e portanto deve-se lançar mão de modelos matemáticos de turbulência, acrescentando termos as equações anteriormente citadas.
Os modelos de turbulência levam em conta variáveis estatisticas, pois escoamentos turbulentos são altamente caóticos, e com isto há a necessidade de ferramentas estatisticas para representar os escoamentos turbulentos.
Há diversos modelos de turbulência, tais como o modelo K-ε, dos tensores de Reynolds, o de grandes escalas e outros.
O modelo matemático para os diversos tipos de escoamentos, tais como os escoamentos multicomponentes, é estabelecido com base nas equações de Navier-Stokes, conservação da massa e da energia, contudo, nos escoamentos multicomponentes, deve-se ter um fator de correção nestas equações levando em conta a influência de cada componente no escoamento. Este fator que leva em conta esta influência é a fração volumétrica de cada componente. E devem ser resolvidas todas equações para cada componente.
As equações são escritas na forma tensorial a seguir:
- Equação de Navier-Stokes modificada:
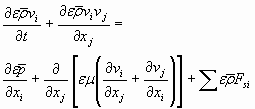 (1)
(1)
- Equação da conservação da massa modificada:
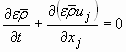 (2)
(2)
Simplificando esta equação, considerando que o escoamento é incompressível:
![]() (3)
(3)
onde o termo 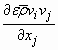 representa
o termo não linear (termo convectivo) e
representa
o termo não linear (termo convectivo) e 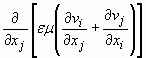 representa
o termo difusivo.
representa
o termo difusivo.
Já, o termo da fração volumétrica é definido como sendo:
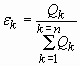 (4)
(4)
sendo que k representa a fase que esta sendo analisada. Quando o escoamento é monocomponente, a fração volumétrica tem o valor unitário, pois somente um componente é analisado e resolvido.
ACOPLAMENTO PRESSÃO-VELOCIDADE
Na formulação incompressível, o fato de r não variar com P introduz um forte acoplamento entre a pressão e a velocidade, causando dificuldades para a solução do sistema de equações. O objetivo, então, é determinar um campo de pressões que, quando inserido nas equações do movimento, origine um campo de velocidade que satisfaça a equação da conservação da massa.
Existem diferentes métodos utilizados para fazer o acoplamento Pressão-Velocidade, tais como o SIMPLE, SIMPLEC, SIMPLER, o Método dos Passos Fracionados com malhas deslocadas (figura 1), é descrito a seguir.
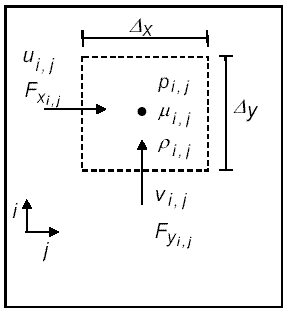
Figura 1: Esquema de malhas deslocadas
Método dos Passos Fracionados
Neste método a equação do movimento é resolvida para as componentes da velocidade e uma equação de Poisson é resolvida para a pressão.
Para correção de pressão, utilizou-se o método não iterativo, que consiste em estimar um campo inicial de velocidade com base em campos de pressão, de velocidades da iteração anterior. Com estes campos de velocidades estimados calcula-se o campo da correção da pressão e em seguida, obtém-se o novo campo de velocidades que satisfaz à equação da continuidade.
As estimativas das componentes da velocidade, que são feitas através dos campos de pressão e velocidades, calculados na iteração anterior, são dadas conforme equação (5):
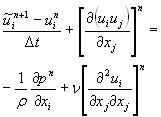 (5)
(5)
Subtraindo-se a equação (1) da equação (5), ambas já discretizadas, para escoamento monofásico, obtêm-se:
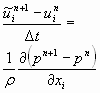 (6)
(6)
Aplicando a conservação da massa, têm-se:
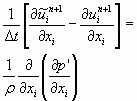 (7)
(7)
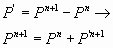 (8)
(8)
Rescrevendo a equação (7) de modo a obedecer a conservação da massa:
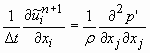 (9)
(9)
Sendo ![]() (8)
a correção do campo de pressão, obtêm-se:
(8)
a correção do campo de pressão, obtêm-se:
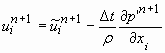 (10)
(10)
Portanto, os passos a seguir na realização do método dos Passos Fracionados são os seguintes:
- Estima-se valores iniciais para os campos de velocidades e pressão;
- Resolve-se explicitamente a equação (7) para se obter a estimativa dos campos de velocidades;
- Com os campos de velocidades estimadas, calcula-se a correção de pressão através da equação (9);
- Com o campo de correção de pressão calcula-se explicitamente os campos de velocidades através da equação (10) e corrige-se o campo de pressão com a equação (8);
As equações para as velocidades podem ser discretizadas de forma explícita pelo método das Diferenças Finitas.
O sistema linear, originado da equação de Poisson para a correção de pressão, pode ser resolvido com diferentes métodos de solução, tais como o MSI (Modified Strongly Implicit Procedure) desenvolvido por Schneider e Zedan (1981), Gauss-Seidel, Gradiente Conjugado e outros.
Os termos convectivos e os termos difusivos podem ser discretizados por Diferenças Centradas (CDS) como mostrado nas equações abaixo.
- Termos convectivos
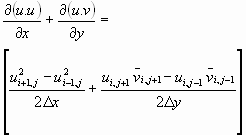 (11)
(11)
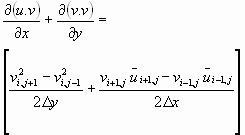 (12)
(12)
onde ![]() e
e
![]() são médias calculadas
da seguinte forma:
são médias calculadas
da seguinte forma:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
- Termos difusivos:
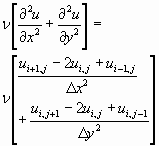 (13)
(13)
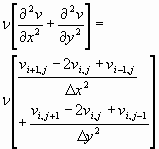 (14)
(14)
Na discretização do gradiente de pressão utiliza-se normalmente o esquema Upwind (BDS):
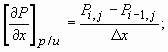 (15)
(15)
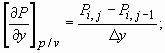 (16)
(16)
Para o termo temporal, podem ser utilizados diferentes esquemas de discretização, tais como o esquema de Euler de 1ª ordem, Adams-Bashford ou outros:
- Esquema de Euler de 1ª ordem
![]() (17)
(17)
- Esquema de Adams-Bashford
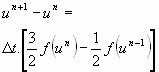 (18)
(18)
A discretização da equação para a correção da pressão (10) resulta:
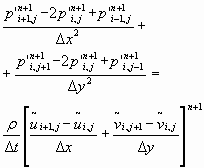 (19)
(19)
Logo, o sistema linear a ser resolvido é:
![]()
cujos coeficientes são dados pelas equações abaixo:
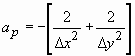 ;
(20)
;
(20)
![]() ;
(21)
;
(21)
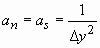 ;
(22)
;
(22)
A turbulência, passados muitos anos de pesquisas, ainda continua sendo um grande desafio para os pesquisadores, pois os escoamentos turbulentos são instáveis e contém flutuações que são dependentes do tempo e do espaço.
Dentre as características mais importantes dos escoamentos turbulentos, destaca-se a multiplicidade de escalas que os caracterizam, desde as maiores estruturas, controladas pela geometria que as geram, até as menores estruturas as quais são controladas pela viscosidade do fluido, além de serem altamente rotacionais.
Muitos acreditam que a física básica da turbulência pode ser descrita pelas equações de Navier-Stokes, as limitações de tecnologia, ainda não permitem a resolução direta para escoamentos turbulentos complexos de interesse tecnológico.
Devido a complexidade deste tipo de escoamento, os pesquisadores lançam mão de ferramentas estatísticas para análise dos mesmos. No entanto, as médias estatísticas não permitem o acesso às mais importantes informações dos mecanismos físicos dos escoamentos, especialmente no que concerne às instabilidades.
Delineando-se o estado da arte do estudo da turbulência, pode-se partir dos trabalhos pioneiros de Reynolds, que estabeleceu os conceitos iniciais de escoamento turbulento, passando por pesquisas que visaram o aprimoramento destes conceitos, tais como Rayleigh, Boussinesq, Prandtl, Von Karman, tem-se em mais de um século de pesquisas o desenvolvimento de diversos modelos de turbulência, os quais alguns serão descritos a seguir.
Modelo K-ε
É um modelo de turbulência de duas equações, baseado na viscosidade turbulenta, (que é idealização conhecida como hipótese de Boussinesq). Este modelo apresenta duas equações de transporte modeladas, separadamente, que são resolvidas, uma para energia cinética (k) e outra para o termo de dissipação da energia cinética (ε), considerando que os tensores de Reynolds são proporcionais aos gradientes de velocidade média, as equações são escritas como se segue:
Para k, conforme equação (21):
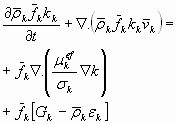 (21)
(21)
Onde:
- Viscosidade efetiva da fase k:
![]() (22)
(22)
- Geração de energia cinética turbulenta no interior da fase k,
![]() (23)
(23)
- Taxa de dissipação de energia cinética turbulenta da fase k,
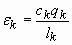 (24)
(24)
A partir destas equações acima, (22, 23 e 24), chega-se a uma expressão para a viscosidade turbulenta da fase k:
![]() (25),
(25),
no qual ![]() ,
é uma constante empírica do modelo.
,
é uma constante empírica do modelo.
Para ε, conforme equaηγo (26)
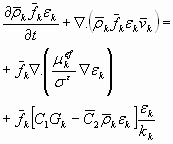 (26)
(26)
No qual as constantes assumem valores aproximados de:
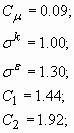 (27)
(27)
A metodologia LES ou método de Simulação de Grandes Escalas é uma metodologia intermediária entre a Simulação Direta (DNS) e a simulação via equações médias de Reynolds (RANS), as quais os outros modelos são baseados.
Esta metodologia filtra as equações de Navier-Stokes e decompõe as variáveis do escoamento em duas partes: uma correspondente a grande escala (resolvida) e a outra a pequena escala (não resolvida ou modelada).
A idéia deste modelo de turbulência é dividir a velocidade em uma média local espacial e as flutuações em torno desta média.
Assim, qualquer variável
do escoamento ![]() pode ser escrita como
sendo,
pode ser escrita como
sendo, ![]() . No qual
. No qual ![]() é
a parte referente a grande escala e é definida através de uma
média volumétrica, assim:
é
a parte referente a grande escala e é definida através de uma
média volumétrica, assim:
![]() (28)
(28)
onde ![]() é
a função filtro.
é
a função filtro.
E o objetivo principal é calcular esta média de maneira mais precisa possível. Isto é perfeitamente tangível, pois baseado na idéia, que as flutuações tem um comportamento randômico, seus efeitos médios no movimento podem ser perfeitamente modelados.
Depois de feito o cálculo da média volumétrica, e desprezando as flutuações de densidade, e introduzindo tensores de escala de sub-malha, podem ser escritas as equações de movimento como sendo:
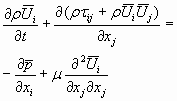 (29)
(29)
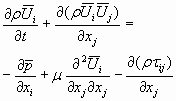 (30)
(30)
com:
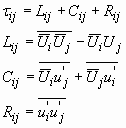 (31)
(31)
Dentro desta metodologia, o modelo mais utilizado é o de Smagorinsky, que pode ser visto como uma combinação da média de Reynolds dada por Lij+Cij=0. E é assumido que os tensores SGS são proporcionais ao módulo da taxa do tensor tensão, do escoamento filtrado de larga escala, mas para fechar a equação, é necessário um modelo de viscosidade. Por meio de análise dimensional, e fazendo uma analogia ao modelo do comprimento de mistura de Prandtl, chega-se ao modelo de Smagorinsky para a viscosidade:
![]() (32)
(32)
onde:
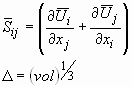 (33)
(33)
E a constante Cs é substituída dependendo do tipo de escoamento e da resolução da malha. Seu valor esta entre um mínimo de 0.065 (escoamentos em canais) e um máximo de 0.25. O valor mais freqüente é 0.1.
Assim, este modelo, é uma técnica em que resolve para escoamentos de larga escala flutuantes e utiliza modelos de turbulência de sub-malhas para os movimentos de pequena escala.
Este modelo é aplicável para escoamentos de altos números de Reynolds, especialmente nos seguintes casos:
- O escoamento é instável;
- É transiente com estruturas coerentes;
- É flutuante, com grandes regiões instáveis;
- A abordagem RANS é falha;
E outros tipos de escoamentos.
Existem diferentes pacotes computacionais para CFD, uns são para construção de geometria, como o ICEM CFD, outros já são pacotes mais completos tais como o FLUENT®, o CFX®.
O ICEM CFD é um pacote que tem como objetivo a construção de diferentes geometrias e malhas numéricas para a simulação.
Figura 2: Tela do ICEM CFD
O usuário pode fazer diferentes geometrias utilizando esta ferramenta.
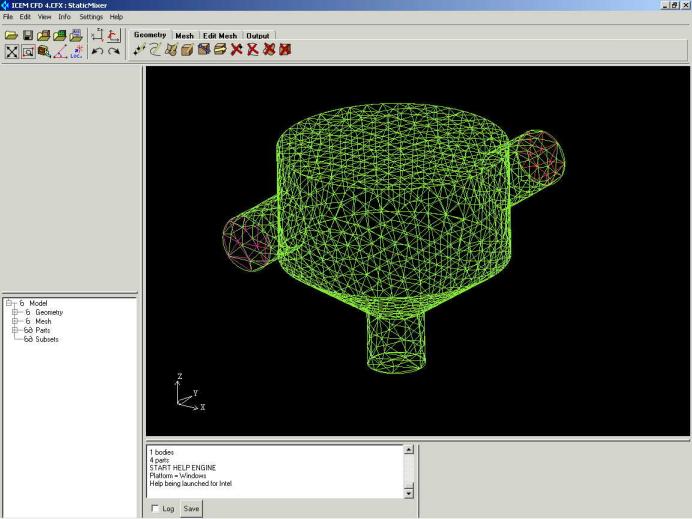
Figura 3: Corpo de um misturador estático com malha gerado no ICEM
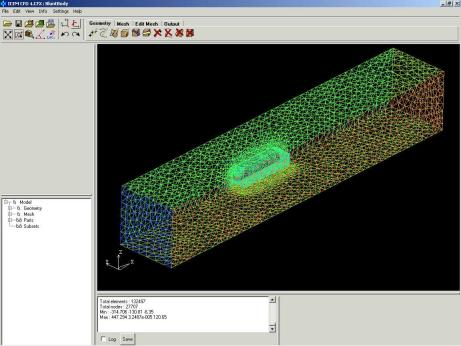
Figura 4: Malha Numérica de um Corpo para Visualização do Escoamento Externo
O CFX® que é um software de CFD integrado, no qual é possível construir a geometria, fazer a malha numérica, ajustar os parâmetros da simulação, resolver e analisar posteriormente, sendo utilizado para a simulação de diversos tipos de escoamentos.
Como é um software comercial, ele é uma "caixa-preta", contudo ele apresenta uma boa interface software-usuário, sendo que o usuário tem a possibilidade de incluir sub-rotinas computacionais escritas em linguagem FORTRAN, e além disto, apresenta a flexibilidade da inclusão de equações para o cálculo de certas variáveis.
- Características do software:
O pacote computacional CFX é composto basicamente de quatro programas, que são:
- O CFX-Build, para a construção das geometrias e da malha numérica;
- O CFX-Pre, para o ajuste dos parâmetros de simulação;
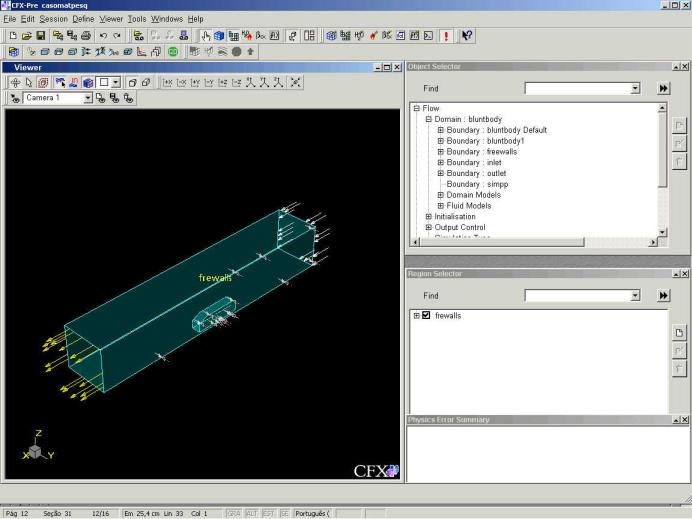
Figura 5: Tela do CFX-Pre
- O CFX-Solver, para a obtenção dos resultados, que podem ser obtidos utilizando um ou vários processadores, isto é, pode ser utilizado em cluster;
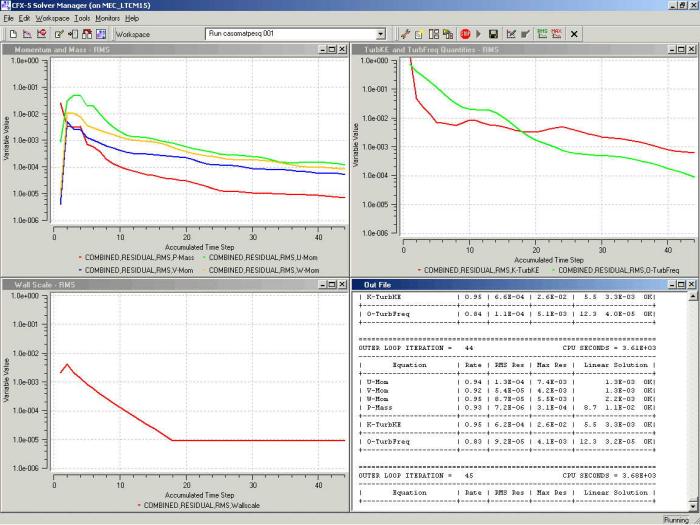
Figura 6: Tela do CFX-Solver
- E o CFX-Post, que é o programa para a análise dos resultados, que processa e apresenta os dados graficamente, podendo o usuário, criar diferentes tipos de imagens gráficas, para melhor análise dos resultados.
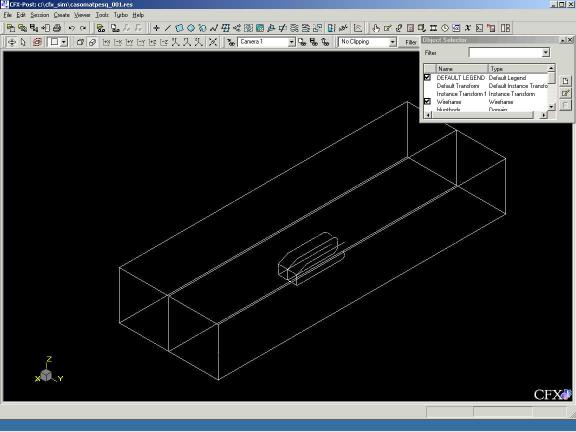
Figura 7: Tela do CFX-Post
- Aplicações:
O CFX e outros softwares comerciais são utilizados nas mais variadas aplicações, dentre elas:
- Indústria petroquímica: na simulação de diversos equipamentos e processos, como por exemplo, o caso da PETROBRAS que utiliza este software para simular diferentes equipamentos e processos, tais como Risers, Ciclones e outros.

Figura 8: Típico Riser de FCC com 60" de diâmetro
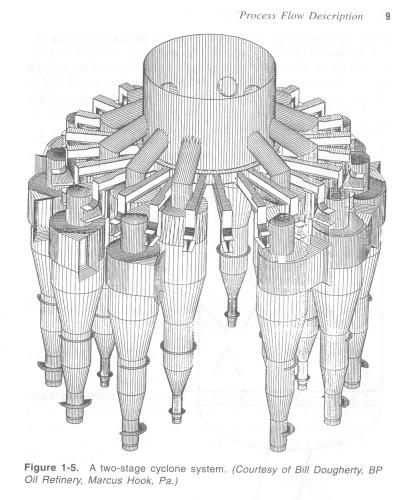
Figura 9: Sistema de Ciclones de Dois Estágios
- Indústria Aeroespacial: na simulação e desenvolvimento de aeronaves, o qual o escoamento é externo, turbinas, onde o escoamento é interno com reação química, que como exemplo se tem a EMBRAER;

Figura 10: Malha Numérica em Diversos Aeroplanos.

Figura 11: Malha Numérica de um Avião Jumbo

Figura 12: Simulação de um Avião Harrier

Figura 13: Simulação de um Avião de Caça F-18

Figura 14: Simulação do Ônibus Espacial
- Indústria automotiva: na simulação e desenvolvimento de automóveis mais aerodinâmicos (escoamento externo), motores (escoamento interno com reação);

Figura 15: Simulação de um Carro de Fórmula 1.
- Escoamentos naturais, como a simulação atmosférica para previsão do tempo e simulação de rios, lagos, para estudos ambientais.
Foi simulado um corpo submetido ao escoamento externo de ar, utilizando o pacote computacional CFX®.

Figura 16: Distribuição de Pressão no Plano XZ

Figura 17: Distribuição de Pressão no Plano YZ, na Posição X = 0
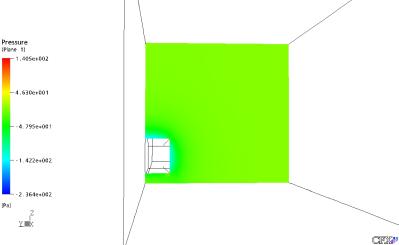
Figura 18: Distribuição de Pressão no Plano YZ, na Posição X = 5
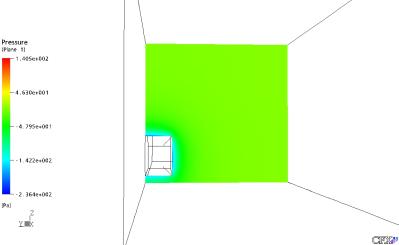
Figura 19: distribuição de Pressão no Plano YZ, na Posição X = 10

Figura 20: Velocidade em X do Gás, no Plano XZ com Y = 0
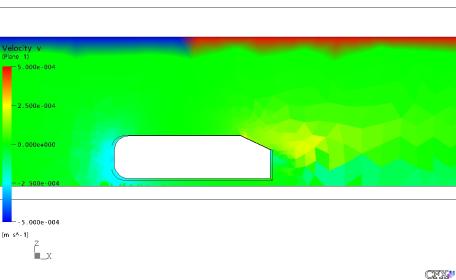
Figura 21: Velocidade em Y do Gás no Plano XZ com Y = 0
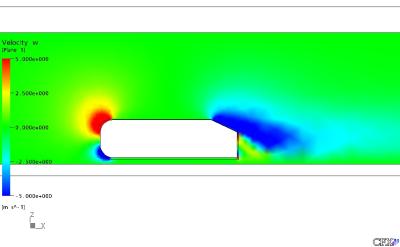
Figura 22: Velocidade em Z do Gás no Plano XZ com Y = 0
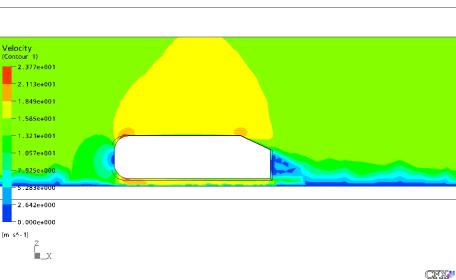
Figura 23: Contorno de Velocidade em Torno do Corpo

Figura 24: Contorno de Velocidade em Torno do Corpo no Plano XY com Z = 5
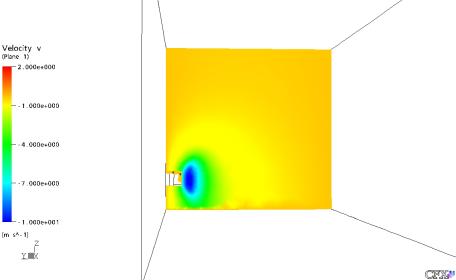
Figura 25: Velocidade em Y no Plano YZ em X = 0
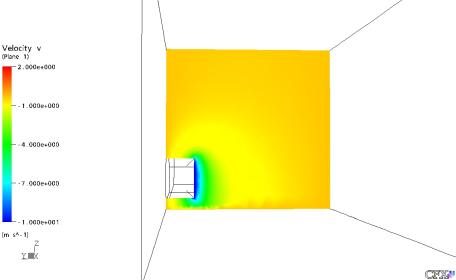
Figura 26: Velocidade em Y no Plano YZ em X = 5
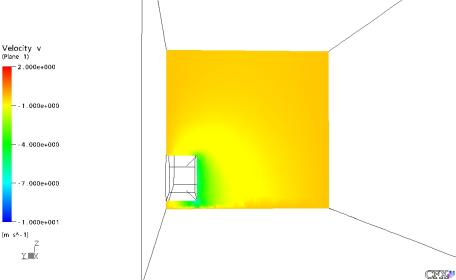
Figura 27: Velocidade em Y no Plano YZ em X = 10
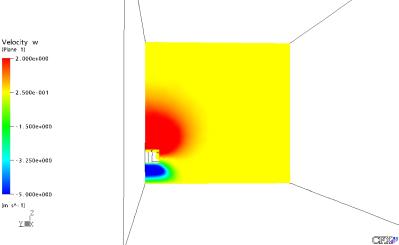
Figura 28: Velocidade em Z no Plano YZ em X = 0
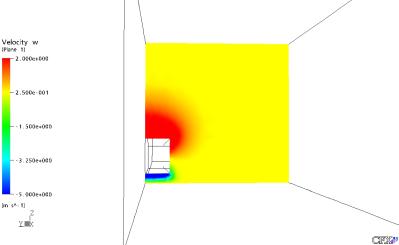
Figura 29: Velocidade em Z no Plano YZ em X = 5
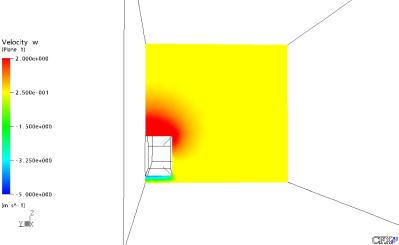
Figura 30: Velocidade em Z no Plano YZ em X = 10
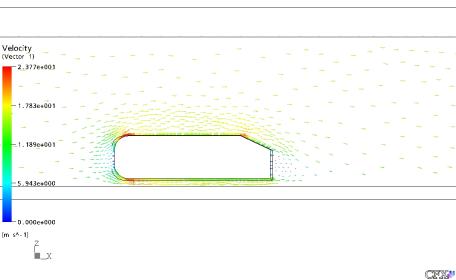
Figura 31: Vetores Velocidade do Gás no Plano XZ em Y = 0
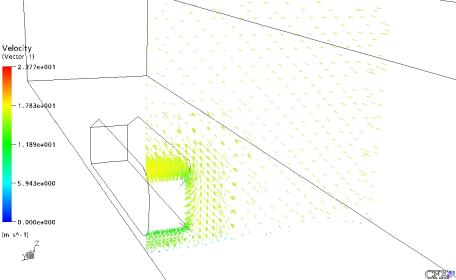
Figura 32: Vetores Velocidade do Gás no Plano YZ em X = 2
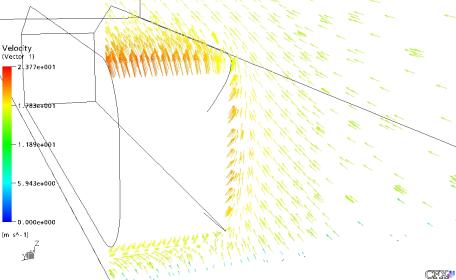
Figura 33: Vetores Velocidade do Gás no Plano YZ em X = 5
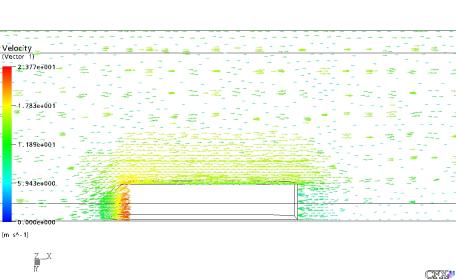
Figura 34: Vetores Velocidade do Gás no Plano XY em X = 0
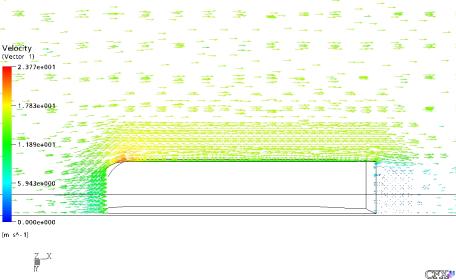
Figura 35: Vetores Velocidade do Gás no Plano XY em Z = 5
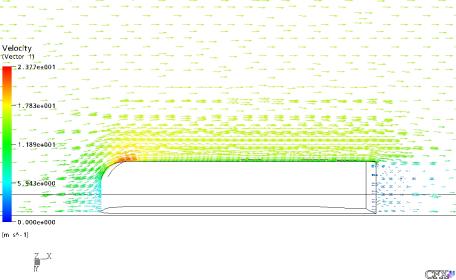
Figura 36: Vetores Velocidade do Gás no Plano XY em Z = 10
Nos dias atuais, as indústrias estão cada vez mais competitivas e, para se manter em um mercado como este são necessários vários investimentos em pesquisa e desenvolvimento de novas tecnologias.
Para isto, as empresas investem em ferramentas computacionais que forneçam resultados precisos e confiáveis. Principalmente, aquelas empresas cujo produto está relacionado com escoamentos de fluidos, isto é, à fluidodinâmica.
As equações que regem a fluidodinâmica de escoamentos industriais são de difícil resolução analítica, como foi mostrado anteriormente. Desta forma deve-se lançar mão de métodos numéricos ou experimentais para a obtenção de resultados de tais escoamentos.
Contudo, a simulação experimental destes, se torna dispendiosa, pois são necessários modelos que representem o equipamento a ser simulado, equipamentos caros, tais como túneis de vento, termopares, anemômetros, e outros equipamentos.
Com isto, a simulação numérica vem se tornando cada vez mais popular, pois é um método barato e de fácil utilização. Existem diversos programas de simulação hoje em dia no mercado, que possibilitam obter resultados muito satisfatórios.
Pode-se ver, através das figuras, que os softwares de CFD são ferramentas poderosas que ajudam cada vez mais os engenheiros. E os resultados obtidos são utilizados para obtenção de dados importantes durante a fase de projeto ou até de otimização de um equipamento industrial.
Contudo, ainda existe um longo caminho a ser percorrido, pois ainda não se tem o entendimento completo de determinados escoamentos, e os modelos matemáticos para tal, ainda não são suficientemente precisos para que se tenham resultados coerentes com a prática.
Além disto, ainda não existe tecnologia suficiente para simulação numérica de grandes equipamentos utilizando a metodologia DNS (Simulação Numérica Direta).
Espera-se que futuros pesquisadores venham contribuir ainda mais com este ramo da ciência que é tão importante, e que sejam desenvolvidos modelos matemáticos que representem bem a diversidade de fenômenos encontrada na natureza e na meio industrial, para que se possa ter um entendimento maior dos mesmos.
Os autores agradecem a FAPEMIG, através do Programa Institucional de Bolsas de Iniciação Científica / PIBIC, pela bolsa concedida ao aluno Matheus Guilherme Reimann Herckert, para a realização deste trabalho. E as várias pessoas que de algum modo participaram deste projeto.
E o aluno Matheus gostaria muito de agradecer ao Professor Dr. Aristeu de lhe ter dado esta grande oportunidade.
ABADIE, Elie, Craqueamento Catalítico, 2ª versão – 1997 – Apostila.
BERNARDO, Sérgio, Segundo Exame de Qualificação de Doutorado: "Estudo dos Escoamentos Gasoso e Gás-Sólido em Ciclones Através da Aplicação de Técnicas de Fluidodinâmica Computacional (CFD)", janeiro/2004 – Apostila.
BIRD, R. Byron, STEWART, Warren E., LIGHTFOOT, Edwin, N., Transport Phenomena, John Wiley & Sons –
COUTINHO, S. A., ALVES, J. J. N., MARTIGNONI, W. P., MORI, Milton, 2003, Modeling and Simulation of Gas-Solid Flows in Riser Reactors.
GIDASPOW, D., HUILIN, Lu, 2003, Hydrodynamic Simulations of Gas-Solid Flow in a Riser, Ind. Eng. Chem. Res., 42, pp. 2390-2398
GIDASPOW, D., HUILIN, Lu, 2003, Hydrodynamicas of Binary Fluidization in a Riser: CFD Simulation Using Two Granular Temperatures, Chemical Engineering Science, 58, pp. 3777-3792.
GIDASPOW, D., HUILIN, Lu, BOUILLARD, Jacques, WENTIE, Liu, 2003, Hydrodynamic Simulation of Gas-Solid Flow in a Riser Using Kinetic Theory of Granular Flow, Chemical Engineering Journal, 95, pp. 1-13
GRANGER, Robert A., Fluid Mechanics, Dover Publications, inc., New York – 1995
GUERMOND, J.-L., ODEN, J. T., PRUDHOMME, S., Mathematical Perspectives on Large Eddy Simulation Models for Turbulent Flows,
LI, Jie, KUIPERS, J. A. M., Gas-Particle Interactions in Dense Gas-Fluidized 711-718. Beds, Chemical Engineering Science, 58, 2003, pp.
LIMTRAKUL, S., CHALERMWATTANATAI, A., UNGGURAWIROTE, Kosol, TSUJI, Yutaka, KAWAGUCHI, Toshihiro, TANTHAPANICHAKOON, Wiwut, (2003), Discrete Particle Simulation of Solids Motions in a Gas-Solid Fluidized Bed, Chemical Engineering Science, 58, pp. 915-921.
LIXING, Zhou, Theory and Numerical Modeling of Turbulent Gas-Particle Flows and Combustion, 1993, Science Press – China.
Manual de Operação do Programa CFX 5.6
Manual de Operação do Programa ICEM 4.2
Manual do CFX-Hexa
MCDONALD, A. T., R. W., Fox, Introdução à Mecânica dos Fluidos, 4 edição, LTC – 1998.
MENTER, F. R., KUNTZ, M., BENDER, R., A Scale-Adaptive Simulations Model for Turbulent Flow Predictions, 41st Aerospace Science Meeting & Exhibit, 2003, AIAA 2003-0767.
NAKAMURA, S., BRODKEY, R. S., Direct and Large Eddy Simulation of the Three-Dimensional Unsteady Flows in The Counter-Jet Mixing Vessel, ASME Fluids Engineering Summer Conference, 2000, FEDSM2000-11007.
PAN, Yingkang, TANAKA, Toshitsugu, TSUJI, Yutaka, Large-Eddy Simulation of Particle-Laden Rotating Channel Flow, ASME 2000 Fluids Engineering Division Summer Meeting, 2000, FEDSM2000-11144.
SILVA FREIRE, Atila P., MENUT, P. P. M., SU, Jian, Turbulência, ABCM, Rio de Janeiro – 2002, pp. 3-48.
SILVA FREIRE, Atila P., MENUT, P. P. M., SU, Jian, Turbulência, ABCM, Rio de Janeiro – 2002, pp. 159-190.
YAMAMOTO, Y., POTTHOFF, M., TANAKA, T., KAJISHIMA, T., TSUJI, Y., Large-Eddy Simulation of Turbulent Gas-Particle Flow in a Vertical Channel: Effect of Considering Inter-Particle Collisions, J. Fluid Mech. (2001), vol. 442, pp. 303-334.
WANG, Meng, MOIN, Parviz, (July 2002), Dynamic Wall Modelling for Large-Eddy Simulation of Complex Turbulent Flows, American Institute of Physics, Volume 14, Number 7.
WILDE, Juray De, MARIN, Guy B., HEYNDERICKX, Geraldine J., 2003, The Effects of Abrupt T-outlets in a Riser: 3D Simulation Using The Kinetic Theory of Granular Flow, Chemical Engineering Science, 58, pp. 877-885.
http://www.esss.com.br/ - acessado em 27/02/2004.
http://www.ansys.com/ - acessado em 27/02/2004.
http://ails.arc.nasa.gov/Images/InfoSys/ - acessado em 27/02/2004.
http://www.fluent.com/ - acessado em 27/02/2004.
MATHEUS GUILHERME REIMANN HERCKERT
matheusreimann[arroba]yahoo.com.br
Faculdade de Engenharia Mecânica – Universidade Federal de Uberlândia – Av. João Naves de Ávila, sn – Campus Santa Mônica – Uberlândia – MG – Brasil – CEP 38400-902
ARISTEU DA S. NETO
aristeus[arroba]mecanica.ufu.br
As opiniões expressas em todos os documentos publicados aqui neste site são de responsabilidade exclusiva dos autores e não de Monografias.com. O objetivo de Monografias.com é disponibilizar o conhecimento para toda a sua comunidade. É de responsabilidade de cada leitor o eventual uso que venha a fazer desta informação. Em qualquer caso é obrigatória a citação bibliográfica completa, incluindo o autor e o site Monografias.com.