Quando dizemos que a filosofia não nos interessa, o que provavelmente fazemos é substituir uma filosofia explícita por outra implícita, isto é, imatura e incontrolada. [...] Esta filosofia caseira [...] supõe que um símbolo, tal como uma equação, possui significado físico somente à medida que diga respeito a alguma possível operação humana. Isto equivale a se considerar a totalidade da física como se referindo a operações, principalmente medições e cálculos, e não à natureza, o que implica num retorno ao antropocentrismo prevalecente antes do nascimento da ciência.
Mario Bunge [1]
Sumário: Sabe-se, desde as primeiras décadas do século XX, que o elétron, ao contrário de uma carga elétrica clássica, assume, com grande freqüência, um comportamento anômalo quando de sua exploração experimental, chegando mesmo a dar-nos a impressão de tratar-se de uma partícula paranormal. Por vezes parece estar dotado de propriedades que o situam numa outra dimensão ou num universo paralelo ao nosso. Não obstante, aceita-se, tal e qual um dogma travestido de paradigma "kuhniano" [2], sua natureza "maxwelliana". Em outras palavras, excetuando-se tais fenômenos mirabolantes, somente decifrados através da matemática quântica, admite-se, sem qualquer apelo a uma comprovação experimental rigorosamente lógica, que o elétron apresenta um comportamento idêntico ao de uma carga elétrica "coulombiana". Recentemente publiquei uma teoria a respeito do elétron [3] que se apoia na negação do paradigma citado. Neste artigo pretendo resumir, ou até mesmo evoluir, alguns tópicos essenciais da teoria, remetendo, a sua fonte, o leitor interessado nos detalhes axiomáticos ou heurísticos
São inúmeras as experiências realizadas no século XX a sugerir, por um lado, a natureza discreta dos agentes reponsáveis pelos fenômenos eletromagnéticos e, por outro, a natureza não coulombiana destas partículas. Contrapõe-se a estas evidências experimentais, a beleza das equações de Maxwell, frutos de uma teoria que sintetizou e coroou os esforços dos cientistas do século passado ao caracterizarem o que julgavam tratar-se de um fluido: o fluido elétrico. Hoje não há mais porque se pensar em fluidos elétricos; e ao supor que o elétron é a fração elementar da carga elétrica, posto que uma carga elétrica é composta por eletrons, incorre o físico no mesmo erro que um filósofo ingênuo incorreria se admitisse que o átomo tem o formato de um avião, posto que um avião é formado por átomos.
Mas se os eletrons não são cargas coulombianas, como os mesmos conseguem se agrupar a ponto de originar uma carga elétrica que gera um campo elétrico E coulombiano? De que forma eletrons e protons se dispõem, num condutor submetido a uma diferença de potencial, de forma a gerar um campo B dado pela lei de Ampère-Laplace? Qual é o campo de um elétron, e como e porque tais campos se associam assumindo disposições maxwellianas? Dentre os campos maxwellianos: Quais são os lorentzianos? Ou seja, aqueles nos quais um elétron obedece à equação de Lorentz, como se possuísse uma carga elétrica?
A física moderna não responde a estas perguntas; e nem poderia, posto que tanto a teoria da relatividade quanto a física quântica se apóiam no absurdo apontado no parágrafo primeiro desta introdução. Resta-nos então seguir a lógica clássica, e desta forma, nos itens que seguem, procurarei desenvolver o arcabouço matemático necessário para que se possa chegar a um eletromagnetismo fundamentado no conceito de partículas, e não no de fluidos elétricos.
Vamos admitir inicialmente que o elétron possa ser representado matematicamente por sua posição P = P(x,y,z) associada a um versor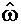 
que retrata aspectos qualitativos de sua estrutura interna, e por um escalar K responsável pela quantificação dos fenômenos eletromagnéticos relacionados ao mesmo. Seja ainda 
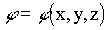um campo definido, em um ponto Q = Q(x,y,z) exterior ao elétron, através da expressão:
|
|
(1) |
Página seguinte  |
|
|
|
Enviado por 