 Página anterior Página anterior |   Voltar ao início do trabalho Voltar ao início do trabalho | Página seguinte  |
O objectivo do nosso trabalho é examinar o grau de desenvolvimento de vários países, cujo denominador comum é a língua oficial, e como um pequeno número de novas variáveis (3 factores ou componentes) podem ser derivadas de 15 variáveis originais.
Quadro i - alguns indicadores de desenvolvimento dos países de língua portuguesa
|
EMV |
TAA |
TEB |
PIB |
PIB1 |
TMI |
PATS |
TMG |
SIDA |
RADIO |
CTI |
TCPU |
TCAP |
ELECT |
CO2 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
Portugal |
74,8 |
89,6 |
81 |
12674 |
6171 |
7 |
99 |
18 |
7,3 |
245 |
30,2 |
1,3 |
-0,1 |
3482 |
5,3 |
|
Brasil |
66,6 |
83,3 |
72 |
5928 |
5928 |
44 |
88 |
13 |
10,0 |
399 |
13,0 |
1,6 |
1,1 |
1954 |
1,6 |
|
Cabo Verde |
65,7 |
71,6 |
64 |
2612 |
2612 |
54 |
30 |
12 |
8,9 |
179 |
10,0 |
3,7 |
2,1 |
55 |
0,3 |
|
São Tomé |
69,0 |
75,0 |
57 |
1744 |
1744 |
62 |
86 |
4 |
3,0 |
271 |
4,2 |
3,2 |
1,8 |
96 |
0,6 |
|
Angola |
47,4 |
42,0 |
30 |
1839 |
1839 |
170 |
15 |
6 |
1,0 |
34 |
1,7 |
4,9 |
3,1 |
173 |
0,4 |
|
Guiné Bissau |
43,4 |
54,9 |
29 |
811 |
811 |
132 |
27 |
12 |
3,4 |
42 |
2,1 |
4,0 |
2,0 |
40 |
0,2 |
|
Moçambique |
46,3 |
40,1 |
25 |
959 |
959 |
133 |
25 |
13 |
12,6 |
38 |
0,9 |
4,7 |
2,5 |
67 |
0,1 |
1 - EMV Esperança média de vida à nascença, em anos (1995)
2 - TAA Taxa de alfabetização de adultos (%) (1995)
3 - TEB Taxa de escolarização bruta conjunta dos 1.º, 2.º e 3.º níveis (%) (1995)
4 - PIB PIB real per capita (dól. PPC) 1995
5 - PIB1 PIB real ajustado per capita (dól. PPC) 1995
6 - TMI Taxa de mortalidade infantil, por 1000 nados-vivos (1995)
7 - PATS Partos assistidos por técnicos de saúde (%) 1996
8 - TMG Total de mulheres no governo (%) 1995
9 - SIDA Casos de SIDA por 100.000 habitantes (1996)
10 - RADIO Receptores de rádio por 1000 habitantes (1995)
11 - CTI Chamadas telefónicas internacionais (minutos por pessoa) 1995
12 - TCPU Taxa de crescimento da população urbana (%) 1995-2015
13 - TCAP Taxa de crescimento anual da população (%) 1995-2015
14 - ELECTR Consumo de electricidade per capita (kilowatt-hora) 1995
15 - CO2 Emissões de CO2 per capita (1000 tons. métricas) 1995
Fonte: PNUD (1998) - Relatório do Desenvolvimento Humano 1998, Trinova Editora, Lisboa.
1.1 - Objectivos da análise factorial / análise de componentes principais
A análise factorial tem sido usada com os seguintes objectivos:
2.2 - Etapas principais na aplicação da análise de componentes principais ou da análise factorial
Podem-se usar programas informáticos para obter a seguinte informação: a lista de variáveis, a matriz de correlação, comunalidades, loadings dos factores, eigenvalues, a percentagem de variância explicada por cada factor e os scores dos factores. Também se podem obter os loadings dos factores baseados em algum tipo de solução rotacional.
2.2.1 - Verificar a matriz de correlação das variáveis
A análise de componentes principais (ACP) e a análise factorial (AF) são técnicas estatísticas aplicadas a um único conjunto de variáveis sobre as quais o investigador está interessado em descobrir aquelas que dentro do conjunto formam subconjuntos coerentes e que são relativamente independentes umas das outras. As variáveis que estejam correlacionadas com outras mas largamente independentes dos outros subconjuntos de variáveis são combinadas em factores. Estes são conceitos para reflectir o processo subjacente que criou as correlações entre as variáveis.
2.2.1.1 - Coeficiente de correlação entre as variáveis
No nosso exemplo, estamos interessados em estudar o grau de desenvolvimento dos 7 países de língua portuguesa. Foram apresentados os vários indicadores, avaliados por numerosas variáveis. Estas variáveis são analisadas individualmente e por outro lado através das correlações entre elas.
A correlação entre as diferentes variáveis pode ser apresentada sob a forma de uma matriz dos coeficientes de correlação entre todas as variáveis (Quadro II).
A Matriz das Correlações mede a associação linear entre as variáveis através do coeficiente de correlação de Pearson. Para se poder aplicar o modelo factorial deve haver correlação entre as variáveis. Se essas correlações forem pequenas é pouco provável que partilhem factores comuns. Pela análise da Matriz de Correlações, quase todas as variáveis se encontram correlacionadas com as restantes variáveis.
Quadro ii - matriz de correlação das variáveis
|
emv |
taa |
teb |
pib |
pib1 |
tmi |
pats |
tmg |
sida |
radio |
cti |
tcpu |
tcap |
elect |
co2 |
|
|
emv |
1.000 |
.928 |
.961 |
.707 |
.751 |
-.945 |
.849 |
.219 |
.168 |
.845 |
.767 |
-.824 |
-.757 |
.644 |
.656 |
|
taa |
.928 |
1.000 |
.966 |
.740 |
.810 |
-.961 |
.883 |
.359 |
.140 |
.882 |
.802 |
-.938 |
-.874 |
.718 |
.687 |
|
teb |
.961 |
.966 |
1.000 |
.789 |
.870 |
-.961 |
.826 |
.392 |
.227 |
.866 |
.849 |
-.906 |
-.828 |
.748 |
.714 |
|
pib |
.707 |
.740 |
.789 |
1.000 |
.898 |
-.750 |
.725 |
.668 |
.198 |
.538 |
.981 |
-.847 |
-.899 |
.980 |
.983 |
|
pib1 |
.751 |
.810 |
.870 |
.898 |
1.000 |
-.780 |
.763 |
.567 |
.297 |
.775 |
.880 |
-.915 |
-.827 |
.923 |
.815 |
|
tmi |
-.945 |
-.961 |
-.961 |
-.750 |
-.780 |
1.000 |
-.845 |
-.467 |
-.346 |
-.830 |
-.827 |
.897 |
.875 |
-.708 |
-.696 |
|
pats |
.849 |
.883 |
.826 |
.725 |
.763 |
-.845 |
1.000 |
.240 |
.116 |
.869 |
.712 |
-.916 |
-.859 |
.751 |
.715 |
|
tmg |
.219 |
.359 |
.392 |
.668 |
.567 |
-.467 |
.240 |
1.000 |
.634 |
.142 |
.692 |
-.520 |
-.660 |
.681 |
.636 |
|
sida |
.168 |
.140 |
.227 |
.198 |
.297 |
-.346 |
.116 |
.634 |
1.000 |
.240 |
.234 |
-.241 |
-.256 |
.236 |
.113 |
|
radio |
.845 |
.882 |
.866 |
.538 |
.775 |
-.830 |
.869 |
.142 |
.240 |
1.000 |
.559 |
-.861 |
-.676 |
.576 |
.447 |
|
cti |
.767 |
.802 |
.849 |
.981 |
.880 |
-.827 |
.712 |
.692 |
.234 |
.559 |
1.000 |
-.856 |
-.915 |
.937 |
.956 |
|
tcpu |
-.824 |
-.938 |
-.906 |
-.847 |
-.915 |
.897 |
-.916 |
-.520 |
-.241 |
-.861 |
-.856 |
1.000 |
.945 |
-.876 |
-.798 |
|
tcap |
-.757 |
-.874 |
-.828 |
-.899 |
-.827 |
.875 |
-.859 |
-.660 |
-.256 |
-.676 |
-.915 |
.945 |
1.000 |
-.902 |
-.892 |
|
elect |
.644 |
.718 |
.748 |
.980 |
.923 |
-.708 |
.751 |
.681 |
.236 |
.576 |
.937 |
-.876 |
-.902 |
1.000 |
.958 |
|
co2 |
.656 |
.687 |
.714 |
.983 |
.815 |
-.696 |
.715 |
.636 |
.113 |
.447 |
.956 |
-.798 |
-.892 |
.958 |
1.000 |
A análise revela tramas de correlação entre as variáveis, que são conceitos que reflectem os processos subjacentes que afectam o grau de desenvolvimento destes países. A variável SIDA é aquela que apresenta menores valores na sua relação com as outras variáveis.
2.2.2 - Distinção entre análise dos componentes principais e análise factorial
Para explorar as possibilidades de redução dos dados construindo um novo conjunto de variáveis baseado nas interrelações da matriz de correlação, existem duas vias: a análise de componentes principais e a análise factorial.
Em ambas as vias, as novas variáveis são definidas como transformações matemáticas dos dados originais. No entanto, no modelo de análise factorial o pressuposto é que as correlações observadas são largamente o resultado de alguma regularidade subjacente dos dados básicos. Especificamente, assume que a variável original é influenciada por várias determinantes; uma parte repartida por outras variáveis conhecida como variância comum; e uma variância única. A última é a residual da relação múltipla, e consiste na variância contada por influências específicas para cada variável e também aquela que diz respeito à quantificação dos erros (resíduos).
Em contraste, a análise de componentes principais não faz suposições subjacentes acerca da estrutura das variáveis originais, nem formula hipóteses, com um elemento de variância única por variáveis individuais (Quadro III).
Quadro iii - visão simplificada dos tipos de análise factorial
|
ETAPA |
TIPOS DE OPÇÕES |
TERMINOLOGIA |
|
Matriz de correlação |
(a) Entre variáveis (b) Entre indivíduos |
R-factorial Q-factorial |
|
Extracção do factor inicial |
(a) Factores definidos (componentes) (b) Factores deduzidos |
Componentes principais Análise de factores |
|
Rotação dos factores |
(a) Não correlacionados (b) Correlacionados |
Ortogonal Oblíqua |
2.2.2.1 - Principais diferenças entre os dois em termos de pressupostos e resultados
O modelo de Componentes Principais supõe um sistema fechado onde toda a variação estatística das variáveis é explicada pelas próprias variáveis. De facto, usa-se uma solução de componentes principais na estimativa das comunalidades (por exemplo no Quadro II), quando se assume a unidade na diagonal da matriz de correlação. Esta tem em conta elevadas correlações entre todas as variáveis, com altas variâncias comuns e baixas variâncias únicas.
Estatisticamente, o modelo de componentes principais é favorecido pela fácil solução para o problema das comunalidades.
O modelo de Factores comuns tem problemas em relação à estimação das comunalidades, mas ao contrário dos componentes principais este não assume um sistema fechado. É este aspecto que o torna tão atractivo para os geógrafos, que lidam com situações onde se torna totalmente irreal assumir um modelo fechado. Assim, na maioria dos nossos estudos, este é o melhor quando não se colectaram todas as variáveis e quando existe algum erro de medida. A análise factorial permite, desta maneira, que os problemas sejam tidos em conta e que a variância que não é explicada pelos factores possa ser descrita como um termo de erro residual.
2.2.2.2 - Critérios de selecção de um modelo
Postas aquelas diferenças, passemos a considerar os critérios para seleccionar um modelo em detrimento do outro.
Foi dito que, sob certas condições, ambos os modelos, davam soluções muito semelhantes e funcionavam igualmente bem. Por exemplo, quando todas as correlações entre as variáveis originais são altas e as comunalidades de uma foram plausivelmente estimadas, então existirão pequenas diferenças entre as duas soluções. Em alternativa, se existem algumas variáveis na matriz de correlação que têm baixas correlações, a substituição da unidade na diagonal será uma sobre estimação, e as duas soluções provavelmente darão resultados diferentes.
Assim, a abordagem factorial é a mais realista para problemas onde algum erro de medida deve ser incluído e alguma estrutura subjacente é tida em conta acerca das relações entre as variáveis. Ao contrário, o modelo de componentes principais trata de casos mais limitados, em que a estrutura subjacente não é visada e cujo principal objectivo é puramente o da redução dos dados (Quadro IV).
Claramente, por tudo aquilo que foi dito, a análise factorial providencia um modelo mais compreensivo para as necessidades da investigação. No nosso caso, utilizámos o modelo de componentes principais, pois existem elevadas correlações entre as variáveis e o principal objectivo do trabalho é a redução dos dados.
Quadro iv - características básicas da análise factorial e análise de componentes principais
|
COMPONENTES PRINCIPAIS |
ANÁLISE FACTORIAL |
|
|
Características |
(a) Assume um sistema fechado, sem pressupostos acerca da estrutura subjacente das variáveis; (b) Identifica somente a variância comum entre as variáveis. |
(a) Pressupostos realistas no que concerne à medida dos erros; (b) Permite procurar a estrutura das variáveis; (c) Identifica a variância comum e a variância única entre as variáveis. |
|
Melhores condições |
Usualmente, se a correlação entre as variáveis é elevada e existe um elevado número de variáveis, somente uma redução simples dos dados é requerida. |
Como para os componentes principais, mas também funciona com uma pequena matriz de variáveis e permite um vasto raio de acção da análise bem como redução de dados. |
Existem dois problemas principais associados à entrada de dados nos programas de análise factorial. O primeiro diz respeito à possível necessidade em transformar os dados originais, quando a normalização dos dados é requerida. Isto deve ser requerido quando as estatísticas inferenciais são usadas como parte da análise factorial. Neste caso, então, idealmente cada variável deve ser controlada pela normalidade e transformada se necessário. Obviamente, se estão envolvidas muitas variáveis, então, este tipo de exercício torna-se extremamente moroso, e, nestas circunstâncias, alguns geógrafos são tentados a empregar a mesma transformação para todas as variáveis. Se inferências não foram feitas então é provavelmente melhor não transformar os dados originais, desde que tais mudanças levem a interpretações obscuras e complicadas.
Na literatura geográfica a decisão de que os dados devem ser transformados ou não é tudo menos clara. Provavelmente, de grande importância é a selecção das variáveis a serem usadas na análise factorial. Obviamente, esta selecção está dependente do tipo de estudo a ser concretizado e da validade dos dados. Isto deve ser pressionado, todavia, que a estrutura dos factores finais deve ser determinada pela qualidade e o tipo de variáveis usadas.
Finalmente, podemos voltar a nossa atenção para a questão de quantas variáveis devem ser incluídas. O efeito de incluir um largo número de variáveis que medem características similares e estão altamente correlacionadas umas com as outras é apenas para aumentar a proporção total de variância que um factor particular consideraria.
2.2.3 - Verificação das comunalidades
As comunalidades são a proporção de variância tida em conta pelos factores comuns.
No entanto, as comunalidades são também os valores usados na diagonal na matriz de correlação, i.e., substituem os valores por um na matriz de correlação das variáveis.
Nesta matriz, as comunalidades são definidas como a correlação de cada variável consigo própria devido, à parte dos elementos comuns, somente esta é a parte da variável comum a outras variáveis. No nosso exemplo usamos o valor um, mas outras estimativas podem ser utilizadas. Como tal, isto produz um raciocínio circular, desde que a comunalidade é a soma do quadrado dos loadings dos factores que não são conhecidos até que os factores tenham sido determinados.
|
variável |
inicial |
extracção |
|
emv |
1.000 |
0.916 |
|
taa |
1.000 |
0.959 |
|
teb |
1.000 |
0.949 |
|
pib |
1.000 |
0.984 |
|
pib1 |
1.000 |
0.871 |
|
tmi |
1.000 |
0.943 |
|
pats |
1.000 |
0.881 |
|
tmg |
1.000 |
0.953 |
|
sida |
1.000 |
0.967 |
|
radio |
1.000 |
0.940 |
|
cti |
1.000 |
0.967 |
|
tcpu |
1.000 |
0.953 |
|
tcap |
1.000 |
0.930 |
|
elect |
1.000 |
0.962 |
|
co2 |
1.000 |
0.977 |
No entanto, os factores não podem ser calculados a partir da matriz de correlação até que as comunalidades tenham sido inseridas. Este problema é resolvido por programas através do uso de procedimentos interactivos baseados em estimativas de comunalidades (Quadro V).
2.2.4 - Importância relativa dos componentes
Os loadings podem ser tratados como coeficientes de correlação, e todavia, o quadrado de cada valor é a proporção de variância na variável individual que está associada com o componente. Tomados juntamente, estes loadings dos quadrados dos componentes representam a variância total tida em conta pelo factor, que se designa por "eigenvalue".
Loadings dos componentes = soma de cada correlação / Ö (soma total de correlações)
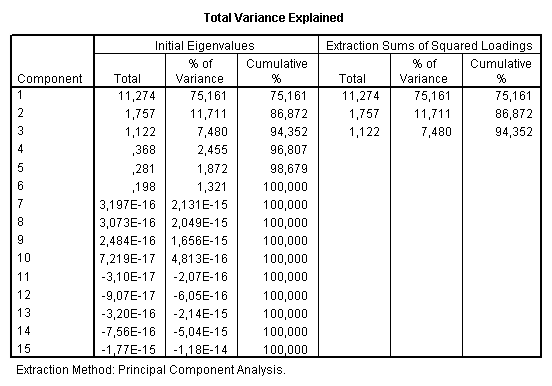
Quadro vi - variância total explicada
Assim, extraímos um novo componente das variáveis originais e medimos a sua variância total ou eigenvalue. Para considerar toda a importância deste eiguenvalue pode-se ter em conta este na variância total na matriz de correlação das variáveis originais. A percentagem de variância pode ser medida pela equação seguinte, e é às vezes referida como a percentagem tida em conta pelo componente:
Percentagem de variância = (h1/n) * 100
em que:
h1 = eigenvalue do componente 1
n = número de variáveis originais
A partir do Quadro VI, podemos ver que no nosso exemplo, o primeiro componente tem em conta 75,2% da variância total. No entanto, este primeiro componente não tem em conta toda a correlação das variáveis originais.
O próximo passo é deduzir um segundo componente para explicar a restante variância. Isto concretiza-se através da subtracção do que pode ser tido em conta pelo primeiro componente a partir da matriz de correlação original.
Contudo, deve ser salientado que o segundo componente é o subtotal das partes das variáveis não tidas em conta pelo primeiro componente, e é ainda ortogonal ou não correlacionado com ele.
Este processo é repetido até que se produza um futuro conjunto de componentes que tenha em conta a correlação das variáveis originais.
2.2.5 - Matriz de loadings ou matriz de cargas rodadas
Consideremos as relações entre as 15 variáveis dadas pela matriz de correlação das variáveis, no Quadro II. A partir desta informação é possível calcular um componente comum, como uma função da raiz quadrada da soma das suas correlações mútuas. A relação entre cada variável com o componente pode ser calculada dividindo cada total de correlação da variável pela raiz quadrada da soma total de correlações. Na análise factorial e análise de componentes principais estes valores são designados por "loadings" e representam as correlações entre as variáveis originais e o novo factor ou componente.
O quadro seguinte contém a matriz de componentes (não rodados), que contém os loadings entre cada variável e os novos componentes. Como já foi dito, estes loadings representam as correlações entre as variáveis originais e os novos componentes.
Quadro vii - matriz de loadings para o estudo do grau de desenvolvimento (não rodada)
|
Componente_1 |
Componente_2 |
Componente_3 |
|
|
1 - EMV |
.8767 |
-.3723 |
.0912 |
|
2 - TAA |
.9292 |
-.3033 |
.0608 |
|
3 - TEB |
.9409 |
-.2324 |
.0996 |
|
4 - PIB |
.9209 |
.2673 |
-.2544 |
|
5 - PIB1 |
.9302 |
.0754 |
-.0121 |
|
6 - TMI |
-.9313 |
.1745 |
-.2138 |
|
7 - PATS |
.8829 |
-.3180 |
-.0259 |
|
8 - TMG |
.5792 |
.7648 |
.1805 |
|
9 - SIDA |
.2873 |
.4690 |
.8152 |
|
10 - RADIO |
.7995 |
-.4711 |
.2804 |
|
11 - CTI |
.9397 |
.2332 |
-.1725 |
|
12 - TCPU |
-.9724 |
.0860 |
-.0210 |
|
13 - TCPA |
-.9549 |
-.1139 |
.0697 |
|
14 - ELECTR |
.9129 |
.2851 |
-.2185 |
|
15 - CO2 |
.8752 |
.2837 |
-.3610 |
Com estes loadings é possível determinar que variáveis «pesam» ou se relacionam juntamente com os novos componentes.
No nosso exemplo, para o Componente_1 podemos ver que todas as variáveis à excepção da TMI, TCPU e TCPA, pesam positivamente. Contudo, temos outras variáveis (TMG e SIDA) que têm fracos loadings.
O Componente_2 tem um baixo conjunto de loadings e pode ver-se que só relaciona significativamente uma variável original, nomeadamente a TMG (positivamente).
No entanto, uma vez mais algumas outras variáveis podem ser incluídas na estrutura deste componente.
O Componente_3 relaciona-se positivamente e de forma significativa com a variável SIDA.
A partir deste ponto podemos tomar duas decisões. A primeira diz respeito quantos componentes examinámos (neste caso 3) e o segundo relaciona-se com a composição dos componentes. Em ambos os casos, a nossa decisão surge como algo subjectivo por natureza, assim, podemos fazer 3 escolhas numa via mais objectiva?
Observando a selecção do número de componentes pode-se usar os eigenvalues ou a percentagem de variância explicada por cada componente. Assim, um eigenvalue de 1,0 ou mais indica qual o componente que explica mais do total de variância do que uma simples variável.
Quadro viii - valores próprios
|
Valores próprios |
% de Explicação |
% Cumul. de Explic. |
|
|
Componente_1 |
11.2741 |
75.16 |
75.16 |
|
Componente_2 |
1.7567 |
11.71 |
86.87 |
|
Componente_3 |
1.1221 |
7.48 |
94.35 |
No nosso exemplo, os primeiros 3 componentes têm eigenvalues de (11.27, 1.75 e 1.12) respectivamente (Quadro VIII), enquanto que os restantes componentes têm valores inferiores a 1,0.
|
|
Um novo método de determinar o número de componentes a serem usados é através de uma curva. A técnica é baseada em identificar uma distinta quebra na inclinação num diagrama da variância total explicada por cada componente (Figura 1). Esta técnica vem comprovar aquilo que foi apresentado anteriormente. |
O segundo problema, o de identificar a estrutura de cada factor, é mais difícil de resolver, no entanto, alguma objectividade pode ser introduzida nos procedimentos. Por exemplo, um ponto de ruptura pode ser decidido pelos loadings individuais. Por exemplo, determinar valores de 0.3 ou 0.4 para distinguir os loadings dos componentes de significante / não significante.
Alternativamente, a composição de cada factor pode ser determinada através do uso de um conhecimento aprofundado acerca das variáveis e da área de estudo.
Para muitos, o objectivo da análise de componentes principais é definir novas variáveis ou componentes que adequadamente e claramente descrevam o conjunto original de variáveis. O ideal é buscar para uma «estrutura de factor simples» por meio da qual cada variável original pesa muito num componente e pouco no segundo. Infelizmente, o que frequentemente acontece é que a solução inicial derivada de um programa de análise factorial não fornece uma estrutura factorial nítida e clara. Assim, no Quadro VII, temos variáveis que pesam bastante em mais que um componente.
Assim, os componentes não descrevem claramente as variáveis originais. O que precisamos é de uma solução alternativa em que os componentes são rodados de forma a fornecer uma melhor descrição da estrutura das variáveis.
A rotação dos componentes, no entanto, visa a simplificação da matriz de componentes separando significantes grupos de variáveis, sem alterar as suas posições relativas.
A melhor opção disponível quando se selecciona uma rotação é qual delas deve ser usada: ortogonal ou obliqua.
As rotações obliquas não são usadas com frequencia pelos geógrafos, desde que não assumam grupos independentes de variáveis e os resultados são mais difíceis de interpretar.
A maioria dos geógrafos usa soluções de rotação ortogonal na análise factorial. Deve-se, parcialmente, à vasta disponibilidade destas rotações na maioria dos programas estatísticos, e por outro lado, devido ao facto de que estas soluções são de fácil interpretação. As rotações ortogonais são baseadas no pressuposto de que os factores não são relacionados, e o ideal é que cada variável tenha um loading de factor de +/- 1.0 num factor, e zero em todos os outros. A mais usada das rotações é a varimax, no entanto, existem outras (Quadro IX). Aqui só consideramos a técnica de varimax, que se baseia na simplificação das colunas duma matriz de factores ou componentes, por meio disso, maximizando a soma da variância do quadrado dos loadings em cada coluna; daí o nome varimax.
Quadro ix - características de algumas rotações factoriais
|
SOLUÇÕES ORTOGONAIS |
|
|
Quartimax |
A variável pesa mais num factor e quase zero nos outros; Simplifica as linhas da matriz de factores. |
|
Varimax |
Como o Quartimax, mas, simplifica as colunas da matriz de factores. |
|
Equimax |
Busca uma solução de compromisso, simplificando tanto as linhas como as colunas. |
|
SOLUÇÕES ORTOGONAIS |
|
Os factores são considerados para serem correlacionados se existirem correlações nos dados originais. |
Olhemos mais de perto o problema da interpretação e nomeação dos componentes à luz das possíveis soluções atrás referidas. Em muitas circunstâncias é proveitoso começar por considerar não só as variáveis com cada componente, mas também as interrelações. Isto pode ser realizado examinando a matriz de correlação original, que pode comandar a formulação de hipóteses acerca da importância dos grupos de variáveis.
Para ilustrar a utilidade deste pressuposto podemos analisar a matriz de correlação. A partir da matriz de correlação, três grupos principais de variáveis podem ser identificados. O primeiro respeita às variáveis que se relacionam positivamente com o grau de desenvolvimento e estão claramente identificadas; o segundo relaciona-se negativamente, e o terceiro correlaciona-se de uma forma muito fraca.
Através da identificação de cada ligação a tarefa de interpretar os componentes torna-se mais fácil. Assim, se analisar-mos os loadings dos componentes (rotação VARIMAX န Quadro X e Quadro XI), podemos ver o aparecimento destas variáveis em relação a factores específicos.
A etiquetagem de cada componente está, todavia relacionada, com a sua hipótese original e os altos loadings de cada componente. Assim, o Componente_1 pode ser expresso como aquele que se relaciona com o grau de desenvolvimento, quer negativa quer positivamente, e tem a ver com o aspecto demográfico. Assim, o primeiro componente pode ser considerado o componente demográfico nas suas várias vertentes.
O Componente_2, tem a ver com os indicadores de consumo, e por isso pode ser considerado o componente consumo.
No que respeita ao terceiro componente, este está mais indefinido e tem pouca relevância, resumindo os indicadores que não variam de país para país e por isso estão pouco correlacionados, como seja o componente da participação feminina e adversidades ou aspectos negativos da marcha pelo desenvolvimento (em termos culturais) ou da situação de proto-desenvimento ao nível sanitário (pela inexistência de meios de prevenção e luta), como é o exemplo da SIDA.
No entanto, deve ser salientado que a classificação das variáveis foi feita com algum grau de subjectividade.
Quadro x - matriz de loadings rodada (rotação varimax)
|
Componente_1 |
Componente_2 |
Componente_3 |
|
|
1 - EMV |
.8982 |
.3294 |
.0154 |
|
2 - TAA |
.8849 |
.4180 |
.0358 |
|
3 - TEB |
.8592 |
.4464 |
.1078 |
|
4 - PIB |
.4352 |
.8879 |
.0804 |
|
5 - PIB1 |
.6277 |
.6670 |
.1792 |
|
6 - TMI |
-.8464 |
-.4162 |
-.2320 |
|
7 - PATS |
.8371 |
.4217 |
-.0514 |
|
8 - TMG |
-.0106 |
.7253 |
.6533 |
|
9 - SIDA |
.1329 |
.0523 |
.9729 |
|
10 - RADIO |
.9548 |
.1294 |
.1065 |
|
11 - CTI |
.4924 |
.8409 |
.1329 |
|
12 - TCPU |
-.7689 |
-.5882 |
-.1265 |
|
13 - TCPA |
-.6061 |
-.7334 |
-.1563 |
|
14 - ELECTR |
.4278 |
.8748 |
.1184 |
|
15 - CO2 |
.3629 |
.9192 |
-.0063 |
Quadro xi - nova variância explicada
|
Nova variância explicada |
% de explicação |
% cumul. de explicação |
|
|
Componente_1 |
6.7738 |
45.16 |
45.16 |
|
Componente_2 |
5.8139 |
38.76 |
83.92 |
|
Componente_3 |
1.5651 |
10.43 |
94.35 |
2.2.6 - Peso de cada componente (matriz de scores)
Os scores dos componentes permitem medir a relação entre cada observação e os novos componentes.
Como mostrá-mos, isto pode ser útil para os geógrafos na análise de padrões espaciais. Estes scores são valores de cada observação em novas variáveis, e como tal, reflectem a extensão da sua relação com as variáveis originais, e a contribuição que cada nova variável faz à sua variância. Assim, se uma observação tem um valor elevado numa variável original, que por seu lado tem um peso elevado no novo componente, então deverá ter um score elevado para este componente principal (Quadro XII e Figuras 2 e 3).
Quadro xii - matriz de scores (coeficientes dos scores)
|
Componente_1 |
Componente_2 |
Componente_3 |
|
|
1 - EMV |
1.43548 |
-.62327 |
-.05369 |
|
2 - TAA |
1.24173 |
-.39955 |
-.05446 |
|
3 - TEB |
1.13754 |
-.36291 |
.02444 |
|
4 - PIB |
-.65715 |
1.46195 |
-.14522 |
|
5 - PIB1 |
.20498 |
.49002 |
.04277 |
|
6 - TMI |
-1.17773 |
.55051 |
-.18387 |
|
7 - PATS |
1.11673 |
-.22122 |
-.16272 |
|
8 - TMG |
-1.31034 |
1.15741 |
.58772 |
|
9 - SIDA |
.30722 |
-1.11297 |
1.17230 |
|
10 - RADIO |
1.94759 |
-1.31635 |
.11575 |
 Página anterior Página anterior |   Voltar ao início do trabalho Voltar ao início do trabalho | Página seguinte  |
|
|
|